A stochastic process, X₁, X₂,…, for which the value taken by the random variable X_m is, for all m>2, independent of X₁, X₂,…, X_m−2 but may depend on X_m−1. The variable X_m may be described as exhibiting the Markov property. If there is a common finite (or countable) number of possible outcomes for all the X-values then the process is a Markov chain. The term ‘chain’ was used by Markov in his original 1906 description.

In a discrete-time Markov chain the random variables X₁, X₂,…are ordered in time. If X_m=r then the process is said to be in state r at time point m. The Markov property implies that the state occupied at time point m is dependent on the state occupied at time point (m−1) but not on the state occupied at any previous time point.

The probability, p_jk, that a chain in state j at any time point will be in state k at the next time point is called the transition probability and is assumed to be unchanging over time. The square matrix, P, in which p_jk is the element in the jth row and kth column, is the transition matrix. The elements on each row of P sum to 1.

If there is a state that, once entered, can never be left, then this is called an absorbing state (or absorbing barrier or trapping state). Such a state will be indicated by a 1 in the leading diagonal of P.

Denote by p_jk⁽ⁿ⁾ the probability that a chain in state j at any time point will be in state k at n time points later (so that p_jk=p_jk⁽¹⁾). If p_jk⁽ⁿ⁾>0, for some n, j, and k, then state k is accessible from state j and the two states are communicating states. A Markov chain is irreducible if all states communicate with each other.

A state is transient if, starting from that state, the probability of ever returning to it is<1; if the probability is equal to 1 then the state is a recurrent state (or persistent state). A recurrent state with a finite expected time until return is called an ergodic state.

In a stationary chain P(X_m=k) is independent of m for all k. Denoting by p_k the probability of being in state k in a stationary chain, this implies that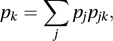for all k.

In a time-reversible stationary chain, the probability of observing a move from state j at time m to state k at time (m+1) is equal to the probability of observing a move from state k at time m to state j at time (m+1):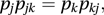for all j and k.

If s refers to a past time, t to the present time, and u to a future time, then, in a continuous-time Markov chain, the probability of being in state l at time u, given that the process is in state k at time t, is independent of the state occupied at time s. If the transition probabilities depend only on the time lag (u−t) rather than on u or t, then the process is a time-homogeneous Markov chain. Examples of continuous-time Markov chains include birth-and-death processes, Brownian motion, queues, random walks, and renewal processes.

Let P_jk(t) denote the probability that a time-homogeneous Markov chain in state j at time 0 will be in state k at time t. The Chapman–Kolmogorov equation states that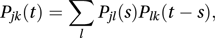for all j and k and for any s in the interval (0, t).