When, as a result of an experiment, values for two random variables X and Y are obtained, it is said that there is a bivariate distribution. In the case of a sample, with n pairs of values (x₁, y₁), (x₂, y₂),…, (x_n, y_n) being obtained, the methods of correlation and regression may be appropriate. Associated with the experiment is a bivariate probability distribution. In the case when X and Y are discrete random variables, the distribution is specified by the joint distribution giving P(X=x_j & Y=y_k) for all values of j and k.

The marginal distribution of X is given by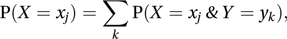and the marginal distribution of Y is given by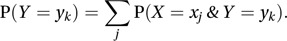If X and Y are independent random variables then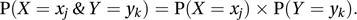The expected values and variances of X and Y are given in the usual way from these marginal distributions. For example,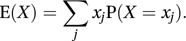The conditional distribution of X, given that Y=y_k, is given by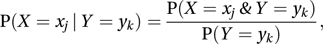and the conditional expectation of X, given that Y=y_k , written as E(X  | Y=y_k), is defined in the usual way as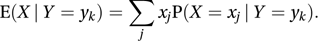The conditional distribution of Y and the conditional expectation of Y, given that X=x_j, are defined similarly.

The mutual information of the variables X and Y is given by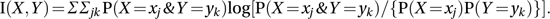The base of the logarithm is usually taken to be 2 (compare diversity index).

In the case when X and Y are continuous random variables, the distribution is specified by the joint probability density function f(x, y) with the property that if R is any region of the (x, y) plane then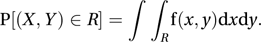The marginal distribution of X then has probability density function (pdf) f_x(x)= and the marginal distribution of Y has pdf f_y(y)=. If the two random variables are independent of one another then f(x, y) is the product of the pdfs of the two marginal distributions. The expected values and variances of X and Y are given in the usual way from these marginal distributions. In this case the mutual information is given by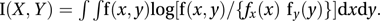

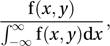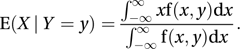The probability density function for the conditional distribution of X, given that Y=y, isandSee also multivariate distribution.