A figure formed by the intersection of a plane and a cone. If the intersecting plane is perpendicular to the axis of a right circular cone, the figure formed is a circle. If the intersecting plane is inclined to the axis at an angle in excess of half the apex angle of the cone it is an ellipse. If the plane is parallel to the sloping side of the cone, the figure is a parabola. If the plane cuts both halves of the cone a hyperbola is formed.
A conic can be defined as a plane curve in which for all points on the curve the ratio of the distance from a fixed point (the focus) to the perpendicular distance from a straight line (the directrix) is a constant called the eccentricity e. For a parabola e=1, for an ellipse e < 1, and for a hyperbola e > 1.
A curve that can be obtained as the plane section of a double cone. The figure shows how an ellipse, parabola, and hyperbola can be obtained.
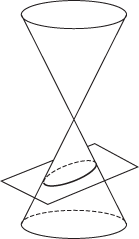
An ellipse
But there are other more convenient characterizations, one of which is by means of the focus and directrix property. Let F be a fixed point (the focus) and l a fixed line (the directrix), not through F, and let e be a fixed positive number (the eccentricity). Then the locus of all points P such that the distance from P to F equals e times the distance from P to l is a curve, called a conic. The conic is called an ellipse if e < 1, a parabola if e = 1 and a hyperbola if e>1. Note that a circle is a conic, but it can only be obtained as a limiting form of an ellipse as e → 0 and the directrix moves to infinity.
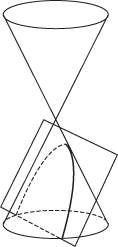
A parabola
In a Cartesian coordinate system, a conic has an equation of the form ax2 + 2hxy + by2 + 2gx + 2fy + c = 0. For an ellipse, parabola, or hyperbola it is the case that h2– ab is negative, zero, or positive respectively. This general degree two equation can also represent degenerate conics.
The polar equation of a conic is normally obtained by taking the origin at a focus of the conic and the direction given by θ = 0 perpendicular to the directrix. Then the equation can be written l/r = 1 + e cos θ (all θ such that cos θ ≠ −1/e), where e is the eccentricity and l is another constant.
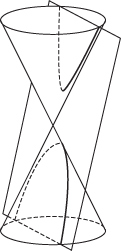
A hyperbola
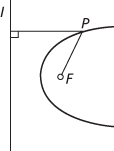
A parabola
http://www.shodor.org/interactivate/activities/ConicFlyer/ An interactive demonstration of a conic section.
- AMIChemE
- amides
- amidol
- amination
- amine
- amine gas treating process
- amines
- amine salts
- Amin Idi (c.1925–2003)
- amino acid
- amino acid racemization
- aminobenzene
- amino group
- aminopeptidase
- aminophenol
- amino sugar
- AMI PCM
- ammeter
- ammine
- ammocoete
- ammonia
- ammoniacal
- ammonia clock
- ammonia-soda process
- ammonite