An inequality which, in different contexts, takes somewhat different forms but in each case essentially states: ‘The length of a side of a triangle is less than the sum of the lengths of the other sides.’ For example, if z1 and z2 are complex numbers, then
This follows from the fact that |OQ| ≤ |OP1| + |P1Q|, where P1, P2, and Q represent z1, z2, and z1 + z2 in the complex plane.
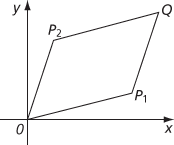
The parallelogram OP1QP2
Likewise, for vectors a and b,
Finally, the inequality for metric spaces
is also referred to as the triangle inequality. Here a,b,c are points in a metric space and d denotes the metric.
The triangle inequality generalizes naturally to finite and infinite series. For example, and the inequality
for absolutely convergent series. A similar inequality holds for integrals
provided that f and |f| are integrable. See also reverse triangle inequality.
See inequality.
- data abstraction
- data acquisition
- data anomaly
- databank
- database
- database administration
- database administrator
- database integrity
- database language
- database management system
- database programming language
- database recovery
- database server
- database system
- data break
- data bus
- data capture
- data cartridge
- data chaining
- data channel
- data cleaning
- data collection
- datacomms
- data communication equipment
- data communications