In formal language theory, a generalization of the notion of language, applying to trees (often called terms in this context) rather than strings. Alphabets are extended to give each symbol an arity, the arity of each symbol dictating the number of subterms, or descendants in the tree, that it has.

For example, let Σ‎ be the alphabet {f,g,a,b} and give arities 2,1,0,0 to f,g,a,b respectively. Then examples of Σ‎-trees and their equivalent representations as Σ‎-terms (or well-formed expressions over Σ‎) are shown in the diagram. A Σ‎-language is now any set of Σ‎-terms. See also tree automaton, tree grammar.

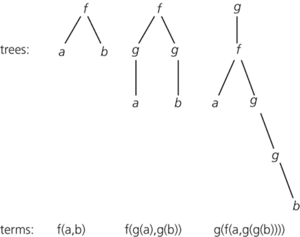
Tree language. Examples of å-trees and å-terms