The distribution of the number of successes in an experiment in which there are two possible outcomes, success and failure. The probability of k successes is:
where p is the probability of success and q (= 1−p) the probability of failure on each trial. These probabilities are given by the terms in the binomial expansion of (p+q)n (see binomial theorem). The distribution has a mean np and variance npq. If n is large and p small it can be approximated by a Poisson distribution with mean np. If n is large and p is not near 0 or 1, it can be approximated by a normal distribution with mean np and variance npq. See also Pascal’s distribution.
The discrete probability distribution for the number of successes when n independent Bernoulli trials are carried out, each with the same probability p of success. The probability mass function is given by , for 0 ≤ r ≤ n. This distribution is denoted B(n, p) and has mean np and variance np(1−p).
The distribution associated with the random variable, X, defined as the number of ‘successes’ in n independent trials each having the same probability, p, of success. The random variable X is said to be a binomial variable and to have a binomial distribution with parameters n and p. This is written as X ~ B(n, p). The mean of this distribution is np and the variance is np (1−p). The probability function is given by
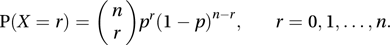 The distribution takes its name from the fact that successive probabilities are the terms in the expansion in ascending powers of p, by the binomial theorem, of (q+p)n, where q=1−p. The first published derivation of the distribution was by Jacob Bernoulli in 1713.
The distribution takes its name from the fact that successive probabilities are the terms in the expansion in ascending powers of p, by the binomial theorem, of (q+p)n, where q=1−p. The first published derivation of the distribution was by Jacob Bernoulli in 1713.As an example, suppose that a computer generates fifteen random integers between 0 and 9 inclusive. The number of these integers that are odd has a B(15, 0.5) distribution. The number that are non-zero has a B(15, 0.9) distribution, and the number that are greater than 7 has a B(15, 0.2) distribution. The diagram shows the graphs of the probability functions for these distributions.
If we note that P(X=0)=qn, successive probabilities can be calculated using the recurrence relation
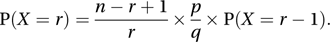 If (n+1)p is not an integer the graph is unimodal, with mode at the (integer) value of r such that and (n+1)p−1 and (n+1)p are both modal values (as in the B(15, 0.5) case illustrated).
If (n+1)p is not an integer the graph is unimodal, with mode at the (integer) value of r such that and (n+1)p−1 and (n+1)p are both modal values (as in the B(15, 0.5) case illustrated).A binomial random variable with parameters n and p may be regarded as the sum of n independent observations of a Bernoulli variable (see Bernoulli distribution) with parameter p. The sum of two independent binomial variables with parameters n1, p and n2, p, respectively, is also a binomial variable, with parameters (n1+n2), p.
For large values of np and nq the normal approximation to the binomial distribution may be used:
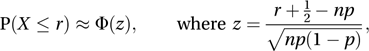 and Φ is the cumulative distribution function for a standard normal variable (see normal distribution). The ‘½’ is a continuity correction. The result, that a binomial distribution with p = ½ may be approximated by a normal distribution, underlies the derivation of the normal distribution by de Moivre in 1733 and is sometimes referred to as the de Moivre–Laplace theorem. For large values of n and small values of p the Poisson approximation to the binomial distribution may be used:
and Φ is the cumulative distribution function for a standard normal variable (see normal distribution). The ‘½’ is a continuity correction. The result, that a binomial distribution with p = ½ may be approximated by a normal distribution, underlies the derivation of the normal distribution by de Moivre in 1733 and is sometimes referred to as the de Moivre–Laplace theorem. For large values of n and small values of p the Poisson approximation to the binomial distribution may be used: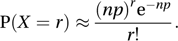 The word ‘binomial’ was used in its mathematical sense in a 1557 text entitled The Whetstone of Witte by Robert Recorde. The ‘binomial distribution’ was so named by Yule in 1911.
The word ‘binomial’ was used in its mathematical sense in a 1557 text entitled The Whetstone of Witte by Robert Recorde. The ‘binomial distribution’ was so named by Yule in 1911.http://www.math.uah.edu/stat/applets/BinomialCoinExperiment.html Applet.
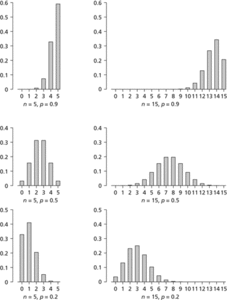
Binomial distribution. The distribution is skewed to the right if p>0.5 and to the left if p<0.5. It is symmetric if p=0.5.
The basic discrete probability distribution for data in the form of proportions. An event, E, can occur with probability p. In a sample of n independent trials the probability that E occurs exactly r times is
(see combination). The distribution is discrete, taking only the values 0, 1, 2,…, n. The mean of the binomial distribution is np and the variance is
In statistics, a discrete probability distribution of the number of outcomes of a particular kind occurring for a set number of trials, where one of two outcomes is possible, each trial is independent, and the probability of a particular outcome is constant.
The distribution of the number of occurrences of a random event as the result of making a number of independent draws, with a known and constant probability of the event occurring each time. If the probability of the event (for example ‘heads’ throwing a coin, or ‘6’ throwing a die) each time is p, and the probability of non-occurrence is (1 − p), the binomial distribution gives the probability of exactly r occurrences in n independent tries, where the r satisfies 0 ≤ r ≤ n. This probability is given by
nCr denotes the number of ways of choosing r objects out of n and is called the binomial coefficient
where r! denotes ‘r factorial’, defined as 0! = 1 and for r > 0
- redeemable security
- redefinition, high/low
- redemption date
- redemption value
- redemption yield
- redeployment
- redevelopment
- Red Feds
- Redfield ratio
- red fluorescent protein
- red fuming nitric acid
- red giant
- Red, Green, And Blue
- Red Guards
- Red Hat enterprise
- Redi, Francesco
- redirection
- redirection script
- red iron ore
- rediscount
- redistributive tax
- redistricting
- red lead
- Redlichiida
- Redlich–Kwong (RK) equation of state