Given a chart φ‎_S : S → ℝ² of a subset S of a surface X, we can define a function f : S → ℝ to be differentiable if f∘φ‎_S^–1: φ‎_S(S) → ℝ is differentiable. Note that this is a map from a subset of ℝ² to ℝ, and we defined differentiability in terms of the local coordinates. The issue arises that this definition might not be consistent between different sets of coordinates.

Given a second chart φ‎_T : T → ℝ² such that S ∩ T = W ≠ ∅, then the transition maps for these two charts are

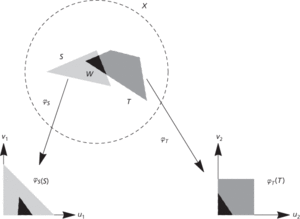
Two charts with intersecting domains. The transition maps connect the darkest regions

Provided the transition maps, which are maps between subsets of ℝ², are differentiable, the preceding definition of differentiability for f can be consistently used for any local coordinates. These ideas can be generalized to define differentiability of maps between any two manifolds.

For a topological manifold the transition maps are automatically continuous functions. But if a manifold has further structure, stronger assumptions must be made of the transition maps in order for the structure to be consistent on the manifold. For example, between Riemann surfaces the transition maps must be holomorphic, and between Riemannian manifolds the transition maps must be isometries.