The discrete probability distribution whose probability mass function is given by Pr(X = 0) = 1−p and Pr(X = 1) = p. It is the binomial distribution B(1, p).
The distribution of a discrete random variable taking two values, usually 0 and 1. An experiment or trial that has exactly two possible results, often classified as ‘success’ or ‘failure’, is called a Bernoulli trial. If the probability of a success is p and the number of successes in a single experiment is the random variable X, then X is a Bernoulli variable (also called a binary variable) and is said to have a Bernoulli distribution with parameter p. The mean of the distribution is p and the variance is p(1−p). The probability function is given by
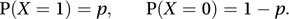A binomial variable (see binomial distribution) with parameters n and p is the number of successes in n independent Bernoulli trials and may be regarded as the sum of n independent observations of a Bernoulli variable with parameter p. The phrase ‘Bernoullian trial’ was used in a 1937 book on probability.
- Maxwell Telescope
- Maxwell–Boltzmann distribution
- Maxwell’s demon
- Maxwell’s equations
- Maxwell’s rule
- Maxwell’s thermodynamic equations
- max‐flow/min‐cut
- Maya
- maya
- Mayall Telescope
- Mayan
- Mayer f-function
- Mayer, Julius Robert von
- Mayer’s test
- Mayflower
- mayfly
- May Fourth Movement
- Maynard Smith, John
- Mayow, John
- Mayr, Ernst Walter
- Mayvillian
- Mazarin, Jules (1602–61)
- Mazzini, Giuseppe (1805–72)
- MB
- Mb