A problem concerned with the comparison of the means of two populations having normal distributions with different variances. The problem was first discussed by B. V. Behrens in 1929. Although Behrens’s method of solution was unclear, his conclusions were confirmed by Sir Ronald Fisher in 1935.
The null hypothesis is that the populations have the same mean, and the suggested solution is an application of the Welch statistic. In this case, the test statistic t is given by
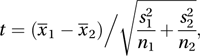where x̄1 and x̄2 are the sample means, n1 and n2 are the sample sizes, and s12 and s22 are the sample variances (using the divisors n1−1 and n2−1). If the populations do have the same mean then t is an observation from an approximate t-distribution with ν degrees of freedom, where ν is taken as the nearest integer to
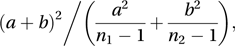where a=s21/ n1 and b=s22 / n2. If n1≤n2, then the above formula ensures that (n1−1)≤ν≤(n1+n2−2).If the populations can be assumed to have the same variance then the problem is simple and the standard t-test (see hypothesis test) is appropriate.
- Dennett, Daniel Clement (1942–)
- Denning, William Frederick (1848–1931)
- denominator
- denormalization
- denotation
- denotational semantics
- denote
- denoting phrase
- de novo pathway
- dense body
- dense gas
- dense matrix
- Dense-medium separation
- dense order
- dense set
- Dense Wavelength Division Multiplexing
- densitometer
- density
- density current
- density-dependent factor
- density dependent factors
- density determination
- density estimation
- density function
- density functional theory