The situation in which a random variable, Y, has expected value g(x1, x2,…, xm), where x1, x2,…, xm are m explanatory variables (see regression) and g is an unknown function. With m=1 and n observations, y1, y2,…, yn, estimation may proceed using a scatterplot smoother such as loess, or by using kernel regression. In the latter case, to estimate the function g in the regression equation
a commonly used procedure employs the Nadaraya-Watson estimator given by
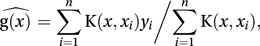
where K is the chosen kernel (see kernel method).
A tool for numerical data analysis where the dependence of the variable of interest on the explanatory variable is estimated without assuming any specific functional form and is entirely driven by the data. The predicted value of the dependent variable at a given point is estimated by smoothing its values over some neighbourhood of this point. This method allows for more flexibility in comparison with a linear regression or a nonlinear regression, but requires large amount of data and intensive computations. See also kernel regression.
- algorithm
- algorithm analysis
- algorithm efficiency
- algorithmic complexity
- algorithmic language
- ALH 84001
- Alhazen (or Abu Ali Al-Hassan Ibn Al Haytham)
- Alhena
- alias
- aliasing
- ALICE
- alicyclic compound
- alidade
- alien
- alienans
- alienation
- alignment
- alimentary canal
- aliorelative
- Alioth
- Ali Pasha, Mehmed Emin (1815–71)
- aliphatic compounds
- aliquant part
- aliquot
- aliquot part