The logarithmic function lnx may be defined for positive x as follows:
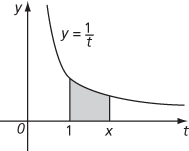
lnx as an area
It can equally be defined as the inverse function of the exponential function. lnx is differentiable and increasing with derivative 1/x.
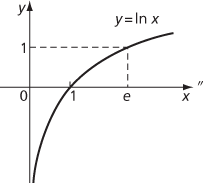
Graph of lnx
Further, lnx = logex satisfies properties (i)–(v) listed under logarithm.
- exclusive dealing
- exclusive disjunction
- exclusive/exhaustive
- exclusive/inclusive disjunction
- exclusive-NOR gate
- exclusive OR gate
- exclusive-OR gate
- exclusive-OR operation
- exclusive union
- ex contradictione quodlibet
- excretion
- ex dividend
- exe
- executable content
- executables
- executable virus
- execute
- execute phase
- execute step
- execution states
- execution time
- executive information system
- executive program
- executive state
- exeligmos