See regression.
The simplest and most used of all statistical regression models. The model states that the random variable Y is related to the variable x by
where the parameters α and β correspond to the intercept and the slope of the line, respectively, and ε denotes a random error. With observations (x1, y1), (x2, y2),…, (xn, yn) the usual assumption is that the random errors are independent observations from a normal distribution with mean 0 and variance σ2. In this case the parameters are usually estimated using ordinary least squares (see method of least squares). The estimates, denoted by α̂ and β̂, are given by
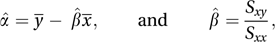where x̄ and y¯ are the means of x1, x2,…, xn and y1, y2,…, yn, respectively, and where
The variance σ2 is estimated by
where .A 100(1−2θ)% confidence interval for β is provided by
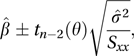where tν(θ) is the upper 100θ% point (see percentage point) of a t-distribution with ν degrees of freedom. A 100(1−2θ)% confidence interval for the expected value of Y when x=x0 is
A 100(1−2θ)% prediction interval for the value y0 of Y when x=x0 is
See also multiple regression model; regression diagnostics; regression through the origin.http://onlinestatbook.com/stat_sim/reg_by_eye/index.html Applet.
In statistics, a comparison of two sets of data to see if there is a linear relationship.
A method in numerical data analysis that models the relationship among variables as a linear function of the unknown parameters. One of the most popular methods of analysing linear regression in econometrics is ordinary least squares; other commonly used methods include least absolute deviation, orthogonal regression, and least median of squares, or robust regression.