For a small quantity x, higher order terms x2, x3,… are yet smaller by comparison. Linearization considers such higher-order terms negligible, so as to simplify an equation with the aim of finding an approximate solution. For example, a simple pendulum that makes the angle θ with the downward vertical satisfies
where denotes acceleration due to gravity and is the length of the pendulum. The solutions involve elliptic integrals. However, for small oscillations θ about the vertical, a linear approximation of sinθ is θ, which gives the equation for simple harmonic motion, and so the exact solution can instead be approximated with trigonometric functions. See linear theory of equilibria.
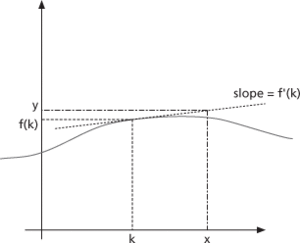
A technique that approximates a function in the vicinity of a given input value as a straight line through the corresponding output value that has a slope equal to that of the function at that point. Given a function f, and a given input value k, then the formula giving linearized output y in terms of input x is
where f′ is the derivative of f with respect to x. See also piece-wise linear function.
Linearization