The statement that f(x) tends to l as x tends to a from the left can be written: f(x)→ l as x → a⁻. Another way of writing this is

The formal definition says that this is so if, given ε‎>0, there is a number δ‎>0 such that, for all x strictly between a−δ‎ and a, f(x) lies between l−ε‎ and l + ε‎. In place of x → a⁻, some authors use x ↗ a. In the same way, the statement that f(x) tends to l as x tends to a from the right can be written: f(x) → l as x → a ⁺. Another way of writing this is

The formal definition says that this is so if, given ε‎>0, there is a number δ‎>0 such that, for all x strictly between a and a + δ‎, f(x) lies between l−ε‎ and l + ε‎. In place of x → a ⁺, some authors use x ↘ a. For example, if f(x) = x−[x], then

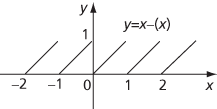
The graph of x – [x]