For a random sample x1, x2,…of observations on a discrete random variable X, the likelihood (a term coined by Sir Ronald Fisher in 1921) is proportional to the product of the probabilities of the individual values:
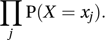When X is continuous, a reported value xj has to be regarded as meaning that the observed value is (in general) in the interval (xj − δ, xj+δ), where δ represents the accuracy of measurement. The likelihood is then proportional to
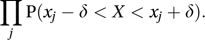If δ is very small then this is approximately proportional to
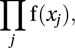where f is the probability density function of X.
The probability that an observation belongs to a probability distribution with parameters θ, considered as a function of the parameters rather than of the observation.
The method of maximum likelihood, originated by R. A. Fisher, estimates parameters in statistical models by maximizing the likelihood of observing the data with respect to the parameters of the model. The values taken by the parameters at the maximum are known as maximum likelihood estimates. This method is computationally equivalent to the method of least squares when the distribution of the observations about their theoretical means is the normal distribution.
- high-order goods and services
- high-order interaction
- high-order language
- high-pass filter
- High Performance File System
- high-performance liquid chromatography
- high ping
- high-plateau crustal type
- high-potassium basalt
- high-powered money
- high-pressure processing
- high recombination-rate contact
- high-resolution electron-loss spectroscopy
- High Sierra standard
- high-speed photometry
- high-speed steel
- high-spin and low-spin complexes
- highspread
- highstand
- highstand systems tract
- high symmetry
- high-technology
- high-temperature superconductivity
- high-temperature superconductor
- high tension