A synonym for correlation.
Two variables are associated if they are not independent, i.e. if the value of one variable affects the value, or the distribution of the values, of the other. Thus, for a human population, height and weight are associated, and so are actual skin-colour and ethnicity. In the case of numerical variables an appropriate measure is the correlation coefficient. In the case of ordinal variables and categorical variables, an alternative measure of association is required.
Yule used the term ‘association’ in his 1900 paper that proposed a measure suitable for the case of two variables each having two categories.
For two categorical variables (A and B having, respectively, J and K categories) a measure with a probabilistic interpretation is Goodman and Kruskal's lambda (λ) suggested by Goodman and Kruskal in 1954. Suppose that we are asked to guess the category of B for the next observation. An intelligent guess would be the category that was the commonest so far (with marginal total equal to f0m , say). Judging by the past data, the probability that our guess will be correct will be P, given by P=f0m/f00, where f00=Σj Σk fjk, fj0=Σk fjk, f0k=Σj fjk and fjk is the frequency of the (j, k) category combination. Suppose now that the next observation belongs to category j of variable A. Our best guess for the category of B now corresponds to the maximum of fj1, fj2,…, fjK. The revised probability of our being correct will be estimated by
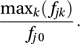 Since the estimated probability of the next observation belonging to category j of A is estimated as fj0/f00, the estimated probability of being correct taking into account the category of A for the next observation is PA, given by
Since the estimated probability of the next observation belonging to category j of A is estimated as fj0/f00, the estimated probability of being correct taking into account the category of A for the next observation is PA, given by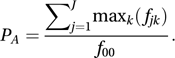 The statistic λ, given by
The statistic λ, given by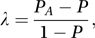 is a measure of the proportional reduction in error resulting from knowledge about A.
is a measure of the proportional reduction in error resulting from knowledge about A.With ordinal variables there are more appropriate measures that take account of the ordering. Let j and j′ be two categories of one ordinal variable, A, and let k and k′ be two categories of a second ordinal variable, B. The quantities S, D and TB are defined in terms of pairs of observations, one belonging to cell (j, k) and the other to cell (j′, k′):
S=the total number of pairs for which, when j>j′, k>k′;
D=the total number of pairs for which, when j>j′, k < k′;
TB=the total number of pairs for which, when j>j′, k=k′.
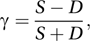 and Somers's dBA, proposed by the sociologist Robert H. Somers in 1962, which is the preferred measure when B is believed to depend on A. The formula is
and Somers's dBA, proposed by the sociologist Robert H. Somers in 1962, which is the preferred measure when B is believed to depend on A. The formula is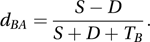
See also two-by-two table.
The combination of molecules of one substance with those of another to form chemical species that are held together by forces weaker than normal chemical bonds. For example, ethanol and water form a mixture (an associated liquid) in which hydrogen bonding holds the different molecules together.
The grouping together of atoms or molecules often in the vapour state or in solution to form conglomerates of high molecular weight. Compare dissociation.
An ecological unit in which two or more species occur in closer proximity to one another than would be expected on the basis of chance. Early plant ecologists recognized associations of fixed composition on the basis of the dominant species present (e.g. a coniferous forest association). Associations now tend to be detected by using more objective statistical sampling methods. See also consociation.
- chirooptical spectroscopy
- Chiroptera
- chirp
- CHISA
- Chisholm, Roderick Milton (1916–99)
- chi-squared contingency table test
- chi-squared distribution
- chi-square distribution
- chi-squared test
- chi-squared variable
- chitin
- chitinase
- Chitinodendron franconianum
- chiton
- Chittenden, Russell Henry
- chivalry
- Chladni, Ernst Florens Friedrich
- Chladni, Ernst Florens Friedrich (1756–1827)
- Chladni figures
- chlamydospore
- chloral
- chloralgal
- chloral hydrate
- chlorates
- chlorenchyma