A differential equation gives information about the rate of change of the dependent variable but not the actual value of the variable. A graph showing the direction indicators of the tangents from which families of approximate solution curves can be drawn are called tangent fields, or direction fields. Curves along which the direction indicators have the same gradient are called isoclines, so in the figure, all the direction indicators at the same value of y are parallel and any horizontal line is an isocline.

The direction field of $\frac{\text{d}y}{\text{d}x}=-y$ is shown in the figure. The general solution to this differential equation is y = Ae^−x and solution curves are shown for the cases where A = −2, −0.5 and 1. In the case where an analytical or algebraic solution is available the tangent fields are not especially useful, but they are powerful tools when no exact solution can be obtained.

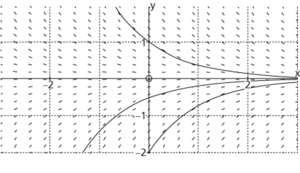
tangent field of $\frac{\text{d}y}{\text{d}x}=-y$