Given two points A and B in the plane and a positive constant k, the locus of all points P such that AP/PB = k is a circle. Such a circle is an Apollonius’ circle. Taking k =1 gives a straight line, so either this value must be excluded or, in this context, a straight line must be considered to be a special case of a circle (see circline). In the figure, k =2.

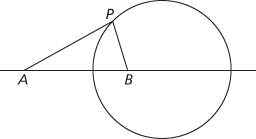
A circle of Apollonius with k = 2