Let f:S → T and g:T → U be functions. With each s in S is associated the element f(s) of T, and hence the element g(f(s)) of U. This rule gives a function from S to U, which is denoted by g∘f and is the composition of f and g. Note that f operates first, then g. Thus g∘f: S → U is defined by (g∘f)(s) = g(f(s)), and exists if and only if the domain of g equals the codomain of f.
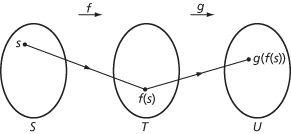
The composition g∘f
For example, suppose that f: ℝ → ℝ and g: ℝ → ℝ are defined by f(x) = 1−x and g(x) = x/(x2 + 1). Then f∘g: ℝ → ℝ and g∘f: ℝ → ℝ both exist, and
The term ‘composition’ is also used for the operation ∘; from the previous example we see ∘ is not generally commutative. Composition of functions is associative: if f: S → T, g: T → U and h: U → V are functions, then h∘(g∘f) = (h∘g)∘f.