A method for the estimation of a probability density function. Suppose X is a continuous random variable with unknown probability density function f. A random sample of observations of X is taken. If the sample values are denoted by x₁, x₂,…, x_n, the estimate (see estimator) of f is given by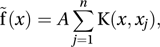where K is a kernel function and the constant A is chosen so that . The observation x_j may be regarded as being spread out between x_j−a and x_j+b (usually with a=b). The result is that the naive estimate of f as being a function capable of taking values only at x₁, x₂,…, x_n, is replaced by a continuous function having peaks where the data are densest. Examples of kernel functions are the Gaussian kernel,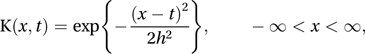and the Epanechikov kernel,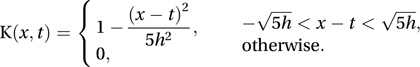The constant h is the window width or bandwidth. The choice of h is critical: small values may retain the spikes of the naive estimate, and large values may oversmooth so that important aspects of f are lost .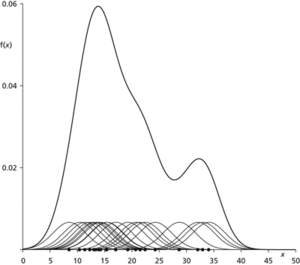

Kernel method. In this case a sample of twenty observations have been generated randomly from a chi-squared distribution with twenty degrees of freedom and a Gaussian kernel with h=3 has been used to generate the kernel density estimate.