A correlation coefficient that can be used as an alternative to Spearman’s rho for data in the form of ranks. It is a simple function of the minimum number of neighbour swaps needed to produce one ordering from another. Its properties were analysed by Sir Maurice Kendall in a paper published in 1938.

As an example, suppose that we have four objects (A–D) and the two orderings (D,B,A,C) and (A,B,D,C). To convert the first ordering into the second using neighbour swaps we could begin by swapping A and B to get (D,A,B,C). Now the swap of A and D gives (A,D,B,C) and then the swap of B and D gives the desired (A,B,D,C). The reordering cannot take fewer than the three swaps used. In a general case with n items to order and a minimum of Q swaps required, τ (which takes values in the interval −1 to 1, inclusive) is given by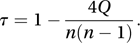An easy way of counting the minimum number of neighbour swaps is as follows. First, write down the items in the order specified by the first ordering. Next, write down the list of ranks assigned to these items by the second ordering. For each number in this list in turn, count how many subsequent numbers are smaller than it. The sum of these counts is Q.