A mapping that projects a sphere onto a plane in a way that preserves the angles at which curves meet but does not preserve either distances or the areas of figures. Thus, a stereographic projection maps all circles on a sphere onto circles.
There are several formulations of what exactly a stereographic projection is. One is to consider the North Pole N of a sphere with a radius of one unit and a plane going through the equator of this sphere. For any point P1 on the surface of the sphere there is a unique line through N and P1 that intersects the plane at a point P2, with P2 being said to be the stereographic projection of P1.
Stereographic projection was known to ancient Greek mathematicians. It has many applications in physical science, including crystallography (particularly X-ray crystallography), optics, relativity theory, quantum mechanics, and electron microscopy. See also gnomonic projection.
Suppose that a sphere, centre O, touches a plane at the point S, and let N be the opposite end of the diameter through S. If P is any point (except N) on the sphere, the line NP meets the plane in a corresponding point P′. Conversely, each point in the plane determines a point on the sphere, so there is a one-to-one correspondence between the points of the sphere (except N) and the points of the plane. This means of mapping sphere to plane is called stereographic projection. Circles not through N on the sphere’s surface are mapped to circles in the plane; circles through N are mapped to straight lines. The mapping is conformal; that is, angles at which curves intersect are preserved by the projection.
Points near N are mapped to points with large modulus, and so it is natural to associate N with infinity in the extended complex plane. In this way we identify the extended complex plane with the Riemann sphere.
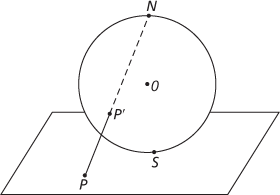
Stereographic projection
http://www.math.union.edu/~dpvc/math/4D/stereo-projection/welcome.html A full description of stereographic projection with two videos to illustrate how it looks.
A mapping that projects a sphere onto a plane in a way that preserves the angles at which curves meet but does not preserve either distances or the areas of figures. One formulation of a stereographic projection is to consider the north pole N of a sphere with a radius of one unit and a plane going through the equator of this sphere. For any point P1 on the surface of the sphere there is a unique line through N and P1 that intersects the plane at a point P2, with P2 being the stereographic projection of P1. Stereographic projections are used in crystallography, particularly X-ray crystallography, and other branches of physical science. See also gnomonic projection.
A two-dimensional graphic representation of a three-dimensional solid object, in which the angular relationships of lines and planes of the object are drawn in terms of their relationship to the great circle formed by the intersection of the equatorial plane with the surface of an imaginary sphere in which the object is contained. Stereographic projections are used widely in structural geology and crystallography.
- dependency ratio
- dependency theory
- dependent equations
- dependent events
- dependent sources
- dependent variable
- dependent variable(statistics)
- dephlegmator
- depiction
- depletable resources
- depleted
- depleted mantle
- depleted uranium
- depletion layer
- depletion-layer photodiode
- depletion mode
- depletion MOSFET
- deployment
- depocentre
- depolarization
- depopulation
- deposit
- deposit account
- deposit feeder
- deposit gauge