Sine is not a one-to-one function, and so not invertible, but ‘inverse sine’ can be defined by choosing a set of principal values. Thus, if y = sin−1 x, then x = sin y, but the converse need not hold. For each x in the interval [−1,1] there is a unique y in the interval [−π/2, π/2] such that x = sin y and this value of y is defined as y = sin−1 x.
Similarly, for real x, y = tan−1 x if x = tan y, and the unique value y is taken from the interval (−π/2, π/2). Also, for x in the interval [−1,1], y = cos−1 x if x = cos y and the unique value y is taken from the interval [0, π].
The notation arcsin, arctan, and arccos for sin−1, tan−1, and cos−1 is also used. Their derivatives are:
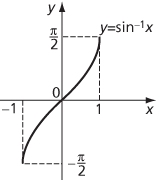
Graph of inverse sine
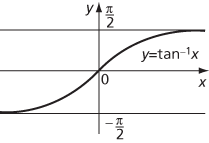
Graph of inverse tangent
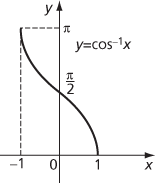
Graph of inverse cosine
- X/OPEN
- XOR
- xor
- XPath
- XPL
- xpols
- X prize
- XPS
- XQuery
- X-ray
- X-ray astronomy
- X-ray background
- X-ray binary
- X-ray bright point
- X-ray burst
- X-ray calorimeter
- X-ray crystallography
- X-ray diffraction
- X-ray diffraction crystallography
- X-ray fluorescence
- X-ray fluorescence spectrometry
- X-ray lithography
- X-ray nova
- X-ray photoelectron spectroscopy
- X-ray photography