If z is a non‐zero complex number and z = x + yi, the (multiplicative) inverse of z, denoted by z⁻¹ or 1/z, is

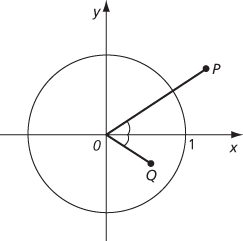
P and its inverse Q

When z is written in polar form, so that z = re^iθ‎ = r(cos θ‎ + i sin θ‎), where r ≠ 0, the inverse of z is (1/r)e^−iθ‎ = (1/r)(cos θ‎−i sin θ‎). If z is represented by P in the complex plane, then z⁻¹ is represented by Q, where ∠xOQ = −∠xOP and |OP|×|OQ| = 1.