For a function f, its inverse function f⁻¹ (or just inverse) is to be a function such that y = f(x) if and only if x = f⁻¹(y). If such a function exists, then it is unique and f is said to be invertible. Suppose that f has domain S and codomain T. To be invertible f: S → T needs to be onto so that every y in T equals f(x) for some x in S. However, any inverse f⁻¹, with domain T and codomain S must uniquely assign such x to this y and so f must also be one‐to‐one. The inverse is then defined by: for y in T, f⁻¹(y) is the unique element x of S such that f(x) = y. Consequently, f is invertible if and only if it is a bijection.

For a real function defined on an interval I, if f is strictly increasing on I or strictly decreasing on I, then f is one‐to‐one and so bijective onto its image.

When an inverse is required for a given function f, it may be necessary to restrict the domain and obtain instead the inverse function of this restriction of f. For example, suppose that f: ℝ → ℝ is defined by f(x) = x²−4x + 5. This function is not one‐to‐one but is strictly increasing for x≥2. Use f now to denote the function defined by f(x) = x²−4x + 5 with domain [2, ∞). The image is [1, ∞) and the function f :[2,∞)→ [1,∞) has inverse f⁻¹: [1,∞)→ [2,∞). A formula for f⁻¹ can be found by setting y = x²−4x + 5 and, remembering that x∈[2,∞), obtaining $x=2+\sqrt{y-1}.$ So, with a change of notation, $f^{-1}\left(x\right)=2+\sqrt{x-1}$ for x≥1.

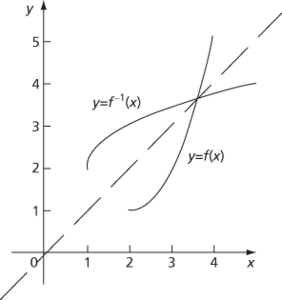
The graph of a function and its inverse

When the inverse function exists, the graphs y = f(x) and y = f⁻¹(x) are reflections of each other in the line y = x. See inverse function theorem, inverse hyperbolic function, inverse trigonometric function, left inverse, right inverse.