The intersection of sets A and B is the set consisting of all elements that belong to both A and B, and it is denoted by A ∩ B (read as ‘A intersect B’ or ‘A cap B’). The term ‘intersection’ is used for both the resulting set and the operation, a binary operation on the set of all subsets of a set. The following properties hold:
(i) For all A, A ∩ A = A and A∩Ø=Ø.
(ii) For all A and B, A ∩ B = B∩A; that is, ∩ is commutative.
(iii) For all A, B and C, (A ∩ B)∩ C = A∩(B ∩ C); that is, ∩ is associative.
Given a family of sets Ai with index set I, then the intersection
consists of those elements x such that x is an element of Ai for all i in I. For the intersection of two events, see event.
The intersection of two events (see sample space) A and B is the event ‘both A and B occur’. It is denoted by A ∩ B. Clearly, for any events A, B, C,
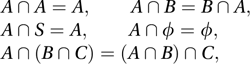 where S is the sample space and ϕ is the empty set. See also Boolean algebra; Venn diagram.
where S is the sample space and ϕ is the empty set. See also Boolean algebra; Venn diagram.The intersection of the n events A1, A2,…, An is the event ‘all of A1, A2,…, An occur’. It is denoted by A1 ∩ A2 ∩…∩ An.
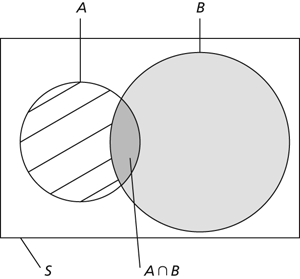
Intersection. This Venn diagram shows the intersection of two events as the overlapping part of the circles that represent the individual events.
In mathematical set theory, the set between two sets A and B that contains only those elements of set A that also belong to set B (and vice versa), written as A∩B.
1. of sets. The set that results from combining elements common to two sets S and T, say, usually expressed as
∩ is regarded as an operation on sets, the intersection operation, which is commutative and associative. SymbolicallyWhen two sets S and T intersect in the empty set, the sets are disjoint. Since the intersection operation is associative, it can be extended to deal with the intersection of several sets.2. of two graphs, G1 and G2. The graph that has as vertices those vertices common to G1 and G2 and as edges those edges common to G1 and G2.
An element belongs to the intersection of two sets, A and B if and only if it belongs to both A and B. The intersection is denoted by A ⋂ B.
- Sakmann, Bert
- Sakmarian
- sakti
- Saladin (1137–93)
- Salam, Abdus
- Salam, Abdus (1926–96)
- salamander
- salami attack
- Salamis, Battle of (480)
- sal ammoniac
- salary
- Salazar, Antonio de Oliveira (1889–1970)
- SALC
- salcrete
- Salem witch trials (1692)
- sales force automation
- sales tax
- salic
- salic horizon
- Salic law
- salicylic acid
- salina
- salination
- saline
- saline giant