Hyperbolic geometry is an example of non-Euclidean geometry. The following model for the hyperbolic plane is due to Poincaré. The set of points comprises the upper half of the complex plane H = {z | Imz>0}, with angles measured as usual, but the hyperbolic distance between two points a,b in H is given by the formula

Note that as w moves towards the real axis, this distance tends to infinity. The isometries of H are the Möbius transformations z ↦ (az + b)/(cz + d), where a,b,c,d are real and ad–bc=1. The first fundamental form has E = G=y^–2 and F = 0, from which the Gaussian curvature can be calculated to equal −1 everywhere.

The geodesics of H are the half-lines which meet the real axis at right angles and the semicircles with centres on the real axis. These geodesics correspond to the lines of Euclidean geometry. The Euclidean parallel postulate states that for any line L, and any point P not on that line, there is a unique line m through P which does not meet L, a so-called parallel. From the figure, we see there infinitely many such parallels in H. There are many other unusual aspects: similar triangles in H are congruent; the area of a triangle equals π‎–α‎–β‎–γ‎, where α‎,β‎,γ‎ are the triangle’s angles; there need not be a circle through three non-collinear points.

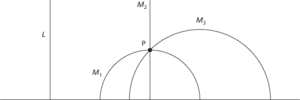
3 parallels through P not meeting L

Given a hyperbolic triangle, with angles α‎,β‎,γ‎ and sides of length a,b,c, then the sine rule states that

the cosine rule states that

with similar versions for β‎ and γ‎, and the dual cosine rule states that

Note that when a,b,c are small enough that the approximations sinha ≈ a and cosha ≈ 1 + a²/2 apply, the sine rule and cosine rule approximate to the Euclidean versions.