A rule to find approximations for the definite integral
Divide [a, b] into n equal subintervals of length h by the partition
where xi+1−xi = h=(b−a)/n, where n is even. Denote f(xi) by fi, and let Pi be the point (xi, fi). Take an arc of the parabola through the points P0, P1, and P2, an arc of a parabola through P2, P3, and P4, similarly, and so on. This is why n is necessarily even. The resulting Simpson’s rule gives
as an approximation to the integral. In general, Simpson’s rule is much more accurate than the trapezium rule, and the error is bounded by
The rule is named after the English mathematician Thomas Simpson (1710–61), though the rule is due to Newton, as Simpson himself acknowledged.
A method for finding an approximate value for an integral, which is usually more accurate than the trapezium rule. Suppose we wish to find an approximate value for . The interval a ≤ x ≤ b is divided into an even number, 2n, of sub-intervals, each of length h=(b − a)/(2n), at points a=x0, x1, x2,…, x2n−1, x2n=b, where xr=(a +rh) for r=0, 1, 2,…, 2n − 1, 2n. Writing yr=f(xr), the integral is approximated by
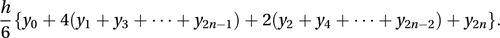
Simpson’s rule gives the exact answer when f is a polynomial of order 3 or less. In general, the error in using Simpson’s Rule is approximately proportional to 1/n4, so that if the number of sub-intervals is doubled then the error is reduced by a factor of 16. Simpson’s rule is based on fitting a quadratic graph in each adjacent pair of sub-intervals such that the graph passes through the points (x2r, y2r), (x2r+1, y2r+1) and (x2r+2, y2r+2).
A numerical integration method used to obtain the approximate value to a definite integral. It is applied to odd numbers of data and is given by:
where S is the width of the intervals between data, F and L are the first and last ordinate, E is the sum of the even-numbered ordinates, and O is the sum of the remaining odd-numbered ordinates.
The approximation
where h = xi+1 − xi. It is used in numerical integration.
- Cantor distribution
- Cantor, Georg (1845–1918)
- Cantor, Georg Ferdinand Ludwig Philipp
- Cantor-Schröder-Bernstein Theorem
- Cantor set
- Cantor’s Diagonal Theorem
- Cantor’s Intersection Theorem
- Cantor’s paradox
- Cantor’s theorem
- Canute
- canyon
- Cao Cao (155–220)
- CAP
- cap
- capabilities
- capability analysis
- capability architecture
- capability constraint
- capability list
- Capability Maturity Model
- capability ratio
- capacitance
- capacitance integrator
- capacitance strain gauge
- capacitance(symbol: C; unit: farad)