A test of a specified circular distribution, adapted from the Cramér–von Mises test, and introduced by Geoffrey Watson in 1961. Denote the n observations by θ₁, θ₂,…, θ_n and write 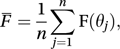where F(θ) is the probability of a value in the interval (0, θ) according to the null hypothesis. The test statistic is U², given by 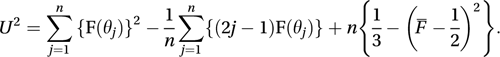A large value of U² leads to rejection of the null hypothesis. A transformed version of U² is provided by U*, given by 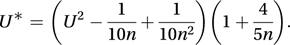The distribution of U* is approximately independent of n. The upper 10%, 5%, 2.5%, and 1% points of U* are 0.152, 0.187, 0.222, and 0.268, respectively.