A line segment is divided in golden section if the ratio of the whole length to the larger part is equal to the ratio of the larger part to the smaller part. This definition implies that if the smaller part has unit length and the larger part has length φ‎, then (φ‎ + 1)/ φ‎ = φ‎/1. It follows that φ‎²−φ‎−1 = 0, which gives $\phi =\frac{1}{2}\left(1+\sqrt{5}\right)$ = 1.6180 to 4 decimal places. This number φ‎ is the golden ratio. A golden rectangle whose sides are in this ratio has throughout history been considered to have a particularly pleasing shape. It has the property that the removal of a square from one end of it leaves a rectangle that has the same shape.

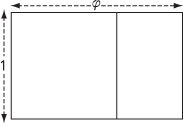
A golden rectangle

http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html#plants Shows the golden ratio in biology and the relationship to Fibonacci numbers.