A rotation of the plane about the origin O through an angle α‎ is the transformation of the plane in which O is mapped to itself, and a point P with polar coordinates (r,θ‎) is mapped to the point P′ with polar coordinates (r,θ‎ + α‎). In terms of Cartesian coordinates, P with coordinates (x,y) is mapped to P′ with coordinates (x′,y′), where

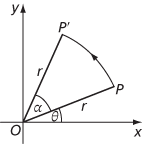
Rotation about O by α‎

This change of coordinates can be represented by the matrix equation

Importantly, distances and angles are still calculated the same using x᾽‎ and y᾽‎ as when using x and y. Note that the matrix is orthogonal and has determinant 1. In 3-dimensional space, an orthogonal matrix with determinant 1 represents a rotation about an axis through the origin.