“generalized linear model”的概念、定义、翻译、参考文献-科学参考

generalized linear model

Statistics

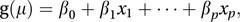
A phrase introduced by Nelder and Wedderburn in 1972 to describe any model that relates μ, the expected value of the response variable (see regression) Y, to a linear combination of the explanatory variables x₁, x₂,…, x_p using the model $generalized linear model$

where β₁, β₂,…, β_p are unknown parameters and g is the link function. Examples of link functions are g(μ) = μ (the identity link), and g(μ) = ln(μ) (the logarithmic link). These correspond to random variables having a normal distribution and a Poisson distribution, respectively.

For different families of models that deal with variation in the parameter p of a binomial distribution:

g(p) = log(p)−log(1−p)	(the logistic link, also called the logit link)
g(p) = log{−log(1−p)}	(the complementary log-log link)
g(p) = −log{−log(p)}	(the negative log-log link)
g(p) = tan{π(p−½)}	(the cauchit link, also called the inverse Cauchy link)
g(p) = Φ⁻¹(p)	(the probit link),

where Φ denotes the cumulative distribution function of the standard normal distribution and here the logarithms are to base e.

Computer

In regression analysis, one of a wide class of model in which the fitted value is a transformation of a linear predictor and the frequency distribution is not necessarily the normal distribution. Apart from the standard linear regression model (see regression analysis), the most important cases are
1. (a) for integer counts, the logarithmic transformation and the Poisson distribution, and
2. (b) for proportions, the logistic transformation and the binomial distribution.
GLMs may be used in regression analysis where inspection of residuals indicates that the distribution is other than the normal distribution, and may also be used to analyse contingency tables.
The analysis uses the method of maximum likelihood, solved by iterative use of weighted least squares estimation.