The process of sampling from the observations in a sample, in order to obtain estimates and confidence intervals for population parameters without making assumptions about the form of the population distribution. Suppose that we have taken a random sample of n observations, and assume, for simplicity, that all the sample values x1, x2,…, xn are different. If we have no other information about the population then the obvious estimate of the population mean, μ, is the sample mean x̄. This is not contentious. However, it is equally true that an unbiased estimate of the probability of the value xj is . In a sense the sample is a surrogate for the population—if we want to know what other samples from the population might have looked like, we can find out by sampling from the sample. This is the process called resampling.
As an example, suppose that we wish to estimate the median of a distribution. We take ten observations and obtain the values
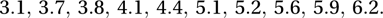
A simple estimate of the median of the distribution is the median that we have observed, namely 4.75. Resampling enables us to derive an empirical confidence interval for this estimate. Using the pseudo-random numbers in the first row of Appendix IX, which begins 07552 37078, we generate a new sample
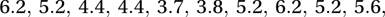
which has median 5.2. Further resampling produces successive sets of ten ‘observations’ with medians 5.6, 4.4, 5.35, 4.4, 3.8, 4.25, 3.95, 4.75, 4.4, 4.75, 4.1. The fifteen resampled medians have mean 4.61 and standard deviation 0.548 so that an approximate 95% confidence interval for the median is (3.5, 5.7). See also bootstrap; jackknife.
Use of repeated sampling from an original data set to obtain certain statistical properties of the data. Methods such as the statistical bootstrap, the jackknife, and cross-validation come under this general heading.