To a first approximation any electron within the body of a metal crystal or fluid may be treated as freely moving.
A single electron within the ionic lattice can be analysed as a particle-in-a-box problem from quantum mechanics. The possible quantum states (ψ) and corresponding energies (E) are obtained on solving the Schrödinger equation for the wave function (ψ). The electron is assumed to be a free particle within the box; outside the box, however, the wave describing the properties of the electron is assumed to have zero amplitude. The Schrödinger equation for this problem is:
where me is the mass of the electron and ∇ is the vector operator del. The solution of this particle-in-a-box problem leads to an expression for the quantum states of the form:
where A is a constant, L is the linear dimension of the crystal, and n1, n2, n3 are integers acting as labels for the different allowed quantum states of the electron in the crystal. The relationship between the energy of the system and the integers n1, n2, n3 is obtained by substituting (2) into (1):
therefore,
where
The wave function ψ(n1, n2, n3) gives the possible ways of fitting the electron wave into the crystal box. However, for each of these ways, the electron also has two orientations of spin. Therefore, when a summation of the total number of states up to a particular n value is calculated, these two degenerate states of spin must be accounted for. The total number of electron states up to a particular n is:
In terms of energy E, G becomes:
where V (=L3) is the volume of the crystal.
The density of states
A useful quantity g(E) is derived from G(E) by considering how G(E) varies with respect to the variable E. g(E) is called the density of states per unit energy interval and is a measure of the number of states within a given arbitrarily narrow interval of energy that the electron may possess:
It is obvious from (6) that the greater the volume the more states can be accommodated up to an energy E. This is a direct consequence of the Heisenberg uncertainty principle—the greater the uncertainty in position, the less the uncertainty will be in the momentum and therefore the kinetic energy.
The density of states g(E) is a useful quantity for analysing the behaviour of electrons in a metal at different temperatures. For example, at absolute zero (0 K), the first electron will be in the lowest energy state, and subsequent electrons will occupy the next higher states. Electrons cannot occupy already filled states because as fermions they obey Fermi–Dirac statistics (see quantum statistics). If there are N electrons to be accommodated within the metal, the lowest N energy states will be filled up to an energy Emax given by:
and
For a monovalent metal, such as sodium or copper, the electrons in the atom are arranged in closed shells with one extra electron in the outside shell. It is this single electron in each atom that is considered free. For a mole of the monovalent metal there will be 6×1023 of these free electrons, i.e. N=6×1023. For a molar volume of about 10 cm3, (8) gives a value of Emax at about 10−18 joules. An application of the theory of equipartition of energy leads to an estimate of electron speeds of the order of 106 m s−1. The free-electron theory therefore predicts a very rapid random motion for conduction electrons inside a metal. Indeed, in this model free electrons are sometimes given the name ‘free electron gas’, because they behave like the atoms or molecules in an ideal gas.
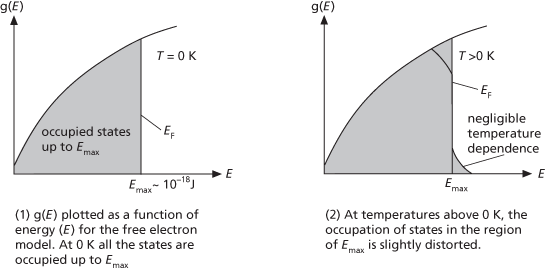
At 0 K the occupation of the lowest 6×1023 states in the mole of metal can be represented in a graph of g(E) (see diagram 1). For temperatures above absolute zero, any variation of the electron energy is provided by the thermal energy of the crystal. The kinetic energies of the electrons are very large compared to these thermal excitations so the energy distribution is only changed very slightly to the form shown in diagram (2).
The Fermi level
The line that delimits the occupied states at a given temperature is called the Fermi level for that temperature and is given the symbol EF. At 0 K, EF=Emax, but it is obvious that this is not the case at all other temperatures. In metals, however, it is sufficient to assume that EF is equal to Emax as the temperature dependence is negligible (see diagram 2). In semiconductors, in general EF ≠ Emax.
- Web developer
- web development
- Web development framework
- Web end
- weber
- Weber, Ernst Heinrich
- Weber, Joseph
- Weber, Mary Ellen (1962– )
- Weber, Max (1864–1920)
- Weber number
- weber(symbol: Wb)
- Weber, Wilhelm Eduard
- Weber, Wilhelm Eduard (1804–91)
- Web feed
- web feed
- Web font
- Web graffiti
- Web guru
- Web log
- Weblog
- web log
- Web log file
- Web logging tool
- Webmail
- web master