Various statistics that give information about the reliability of the estimates of the multiple regression model

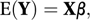
where Y is an n×1 vector of independent and identically distributed response variables, β is a p×1 vector of unknown parameters, and X is an n×p matrix. If β is replaced by its least squares estimate, β̂, the estimated column vector of fitted values, ŷ, is given by

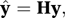
where the n×n matrix H, the hat matrix, is given by

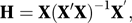
X′ is the transpose of X, (X′X)⁻¹ is the inverse of the matrix X′X, and y is the column vector of observed values. Denote the element in the jth row and kth column of H by h_jk. The fitted value, ŷ_j, for the jth observation, y_j, is given by 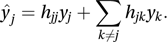Thus there is a direct link between the fitted and observed values in the form of h_jj. This is the leverage: a large value (e.g.>2p/n) indicates an observation having a large influence on the form of the fitted model.

The most obvious guide to the fit of a model are the residuals, e₁, e₂,…, where e_j is given by

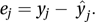
If the random variables have common variance σ² and if s² is an unbiased estimate of σ², then the standardized residual is sometimes defined as e_j/s. However, an unbiased estimate of the variance of e_j is not s² but s²(1−h_jj) and a more appropriate residual (having unit variance if the model is correct) is given by r_j, where 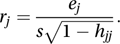This is sometimes called the standardized residual and sometimes the Studentized residual.

The deletion residual is given by

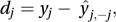
where ŷ_j,−j is the fitted value for observation j based on the fit of the model to all the observations except the observation y_j. Dividing the deletion residual by its estimated standard error, we get the Studentized deletion residual which can be written as 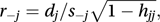where s²_−j is the unbiased estimate of σ² obtained when observation j is omitted. Confusingly, this may also be called the Studentized residual. See also Anscombe residual; deviance residual.

A related influence statistic is DFFITS, which is an abbreviation for difference in fits. For observation j, DFFITS_j is 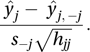The influence statistic DFBETA (difference in beta values) applies the idea embodied in DFFITS to the parameter estimates rather than the fitted values. For β_k, DFBETA_k,−j is 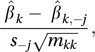where β̂_k is the estimate of β_k from the complete data, β̂_k,−j is the estimate when observation j is omitted, and m_kk is the corresponding diagonal element of the p×p matrix (X′X)⁻¹.

A statistic that usefully combines information about leverage and influence is Cook's statistic, D_j, given by 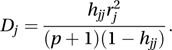This statistic (introduced by Cook in 1977) can also be interpreted as measuring the effect on the parameter estimates of omitting the jth observation. Large values point to possible outliers.