In a finite mixture model the distribution of the random variable X has a known form (e.g. normal distribution), but the values of the parameters of the distribution are not known. Instead, it is known that the vector of the parameters takes one of the values θ1, θ2,⋯, θm with associated probabilities w1, w2,⋯, wm. If, for a continuous random variable, the probability density function of the kth of the possible distributions is denoted by f(x, θk), then the finite mixture distribution of X is given by
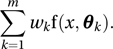 An equivalent result holds for a discrete random variable.
An equivalent result holds for a discrete random variable.
- arcing horn
- arc lamp
- arc length
- arc minute
- arc(of a curve)
- arc(of a digraph)
- arc((of a graph))
- arcosh
- arcover
- arc second
- Arcsecond Space Telescope Enabling Research in Astrophysics
- arc-sine law
- arc-sine transformation
- arc-sinh transformation
- Arctic
- arctic air
- arctic bottom water
- Arctic exploration
- arctic front
- Arctic meteorology
- Arctic Ocean
- Arctic sea smoke
- arctic sea smoke
- Arctic tern
- arc-trench gap