If Y1 and Y2 are independent random variables each having a chi-squared distribution with ν1 and ν2 degrees of freedom, respectively, then the ratio X, given by
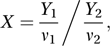 is said to have an F-distribution with ν1 and ν2 degrees of freedom. This may be written as the Fν1,ν2-distribution. Evidently 1/X will have a Fν2,ν1-distribution.
is said to have an F-distribution with ν1 and ν2 degrees of freedom. This may be written as the Fν1,ν2-distribution. Evidently 1/X will have a Fν2,ν1-distribution.The form of the distribution was first given in 1922 by Sir Ronald Fisher, and it is sometimes still referred to as Fisher's F-distribution. In 1934 the distribution was tabulated (see Appendix VII) by Snedecor, who used the letter F in Fisher's honour. The distribution is therefore also referred to as the Snedecor F-distribution. The probability density function f of the Fν1,ν2-distribution is given by
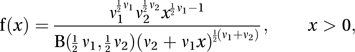 where B is the beta function.
where B is the beta function.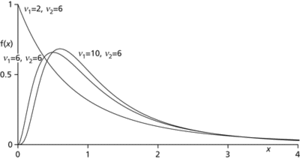
F-distribution. All F-distributions take values from 0 to ∞ and, for ν1, ν2>4, have mean and mode near 1.
The distribution has mean ν2/(ν2−2) provided that ν2>2. The distribution has variance
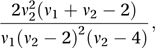 provided that ν2>4. If ν1≤2 there is a mode at 0, otherwise the mode is at
provided that ν2>4. If ν1≤2 there is a mode at 0, otherwise the mode is at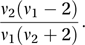 If X has a t-distribution with ν degrees of freedom, then X2 has an F1,ν distribution.
If X has a t-distribution with ν degrees of freedom, then X2 has an F1,ν distribution.
A statistical probability distribution used in the analysis of variance of two samples for statistical significance. It is calculated as the distribution of the ratio of two chi-square distributions and used, for the two samples, to compare and test the equality of the variances of the normally distributed variances.
A continuous distribution described by the probability density function
where p and q are the degrees of freedom. Its moment-generating function does not exist. This distribution is used, for example, in finite sample inference in a linear regression model under the assumption that the underlying random error has normal distribution. For large q, (pF) has asymptotically chi-square distribution with p degrees of freedom.
- photoelectric magnitude
- photoelectric photometer
- photoelectric sensor
- photoelectron
- photoelectron spectromicroscopy
- photoelectron spectroscopy
- photoemission
- photofission
- photogeneration
- photogeology
- photoglow tube
- photogrammetry
- photographic density
- photographic infrared
- photographic magnitude
- photography
- photography and geography
- photoheliograph
- photoheterotroph
- photohydrometer
- photoinhibition
- distributed artificial intelligence
- distributed Bragg reflector laser
- distributed capacitance
- distributed circuit