The one-dimensional infinitely deep quantum well is often used as an example for a simple solution of Schrödinger’s equation in quantum mechanics to illustrate a quantized system. Such a quantum well has a finite width W and in this region the local potential V is zero; outside this region the potential is infinite, thereby constraining the electrons to be inside the well. The solution of Schrödinger’s equation (time-independent) for the quantum well is:

The wavefunction ψ must fall to zero at the edges of the well, x = 0, W, which gives

n is an integer and is a quantum number. The wavefunction ψ is an integral number of half-wavelengths in W, as shown in the diagram. The energies that the electron can have in this system are discrete values – i.e. are quantized; these values of energy are the eigenvalues of the system.

Practical one-dimensional quantum wells can be realized by sandwiching a semiconductor with a narrow energy band gap between wider band gap semiconductors, using molecular beam epitaxy. The energy step at the band edges effectively constrains the electrons (or holes) to the narrow band gap material. Solving Schrödinger’s equation again yields a quantized system, where the electron population is quantized in one dimension, but remains free in the remaining two dimensions, forming a two-dimensional electron gas. This type of well is used as the basis for high electron mobility transistors, and for quantum well semiconductor lasers, where the quantization of electron and hole energy levels produces a narrow line width.

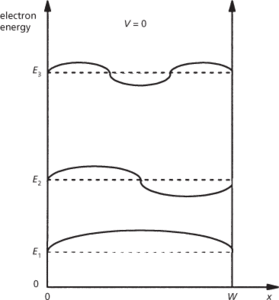
Quantum well, one-dimensional and infinitely deep, showing solutions of Schrödinger’s equation