Ranges of energies that electrons can have in a solid. In a single atom, electrons exist in discrete energy levels. In a crystal, in which large numbers of atoms are held closely together in a lattice, electrons are influenced by a number of adjacent nuclei and the sharply defined levels of the atoms become bands of allowed energy; this approach to energy levels in solids is often known as the band theory. Each band represents a large number of allowed quantum states. Between the bands are forbidden bands. The outermost electrons of the atoms (i.e. the ones responsible for chemical bonding) form the valence band of the solid. This is the band, of those fully occupied, that has the highest energy.
The band structure of solids accounts for their electrical properties. In order to move through the solid, the electrons have to change from one quantum state to another. This can only occur if there are empty quantum states with the same energy. In general, if the valence band is full, electrons cannot change to new quantum states in the same band. For conduction to occur, the electrons have to be in an unfilled band—the conduction band. Metals are good conductors either because the conduction band is not filled or because the conduction band overlaps with the valence band; in either case vacant states are available. In insulators the conduction band and valence band are separated by a wide forbidden band and electrons do not have enough energy to ‘jump’ from one to the other.
In intrinsic semiconductors the forbidden gap is narrow and, at normal temperatures, electrons at the top of the valence band can move by thermal agitation into the conduction band (at absolute zero, a semiconductor would act as an insulator). Doped semiconductors have extra bands in the forbidden gap.
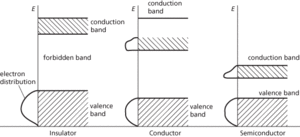
Energy bands.
A range of energies that electrons can have in a solid. In a single atom, electrons exist in discrete energy levels. In a crystal, in which large numbers of atoms are held closely together in a lattice, electrons are influenced by a number of adjacent nuclei and the sharply defined levels of the atoms become bands of allowed energy; this approach to energy levels in solids is often known as the band theory. Each band represents a large number of allowed quantum states. Between the bands are forbidden bands. The outermost electrons of the atoms (i.e. the ones responsible for chemical bonding) form the valence band of the solid. This is the band, of those occupied, that has the highest energy.
The band structure of solids accounts for their electrical properties. In order to move through the solid, the electrons have to change from one quantum state to another. This can only occur if there are empty quantum states with the same energy. In general, if the valence band is full, electrons cannot change to new quantum states in the same band. For conduction to occur, the electrons have to be in an unfilled band – the conduction band. Metals are good conductors either because the valence band and the conduction band are only half-filled or because the conduction band overlaps with the valence band; in either case vacant states are available. In insulators the conduction band and valence band are separated by a wide forbidden band and electrons do not have enough energy to ‘jump’ from one to the other. In intrinsic semiconductors the forbidden gap is narrow and, at normal temperatures, electrons at the top of the valence band can move by thermal agitation into the conduction band (at absolute zero, a semiconductor would act as an insulator). Doped semiconductors have extra bands in the forbidden gap. See illustration.
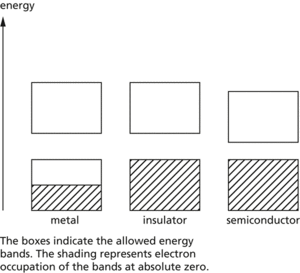
Energy bands
In a crystalline solid, the atoms are close enough together for their energy levels to overlap. Since quantum theory requires each electron in a system to have a unique set of quantum numbers, the individual levels split into bands of energy – known simply as energy bands – to accommodate all the electrons in the solid. Note that the energy bands are not continuous bands of energy, but are ranges of energy containing many closely spaced energy levels.
The formation of the energy bands can be demonstrated mathematically, by solving Schrödinger’s equation of quantum mechanics for an electron moving in the periodic potential V(k) that is associated with the atoms in the crystal. The solutions reveal allowed bands of electron energies, separated by forbidden bands of energy in which there are no travelling wave solutions, indicating that electrons cannot move in the crystal at these energies. The set of energy bands in a particular solid is called the energy-band structure.
At a temperature of absolute zero, all electrons occupy the lowest possible energy levels in the energy-band structure, each electron occupying just one energy level (i.e. having a unique set of quantum numbers). The energy bands are then filled up to a certain energy value, called the Fermi energy or Fermi level, EF. At temperatures above absolute zero, some electrons are able to absorb thermal energy from their surroundings – the crystal; the distribution of electrons in the energy levels is then described by Fermi–Dirac statistics, which yield the probability of finding an electron at a given energy. The way in which the electrons occupy the various bands, and the location of the Fermi energy, provides the fundamental difference between metals, insulators, and semiconductors (see diagram).
In a metal, the highest energy band containing electrons is only partly filled; this allows the electrons to gain kinetic energy from an applied electric field and move in the solid, giving rise to conduction. In an insulator, the highest energy band containing electrons is completely filled; electrons are unable to accept energy from an applied electric field as there are no vacant energy levels within the band for the electrons to move into, so no conduction can take place. A semiconductor is a special class of insulator: while the highest energy band containing electrons is completely filled, the next highest and empty energy band is separated from this band by only a small forbidden energy gap. At absolute zero of temperature a semiconductor is exactly like an insulator, but at higher temperatures a small number of electrons can absorb enough thermal energy to cross the forbidden energy gap to reach the next higher energy band. In this band the electrons are able to accept kinetic energy from an applied electric field, and move to an empty higher energy level, and so conduction can take place. The conductivity is small compared to metals, as only few electrons are able to contribute to the conduction. See also semiconductor.
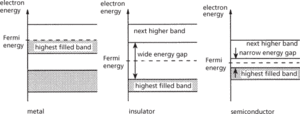
Electron energy bands in solids
- Cambridge Ring
- camcorder
- Camden, Battle of
- camel case
- Camelopardalis
- camera
- cameral
- cameral fluid
- camera phone
- camera ready
- Camerarius, Rudolph Jacob
- Camerata
- Cameron, David (1966)
- Cameron, Kenneth Donald (1949– )
- Cameroon
- Camisards
- camouflage
- cAMP
- Campaign for Nuclear Disarmament
- Campanella, Tommaso (1568–1639)
- Campanian
- Campbell-Bannerman, Sir Henry (1836–1908)
- Campbell bridge
- Campbell, George (1719–96)
- Campbell, Kim (1947– ))