A conic formed by the intersection of a plane with a right circular cone, so that the plane is inclined to the axis of the cone at an angle in excess of half the apex angle of the cone. The ellipse has two vertices, which are joined by a line called the major axis. The centre of the ellipse falls on this line, midway between the vertices. The minor axis is the line perpendicular to the major axis that passes through the centre and joins two points on the ellipse. The foci of an ellipse are two points on the major axis so placed that for any point on the ellipse the sum of the distances from that point to each focus is constant. The area of an ellipse is πab, where a and b are half the major and minor axes, respectively. For an ellipse centred at the origin, the equation in Cartesian coordinates is x2/a2+y2/b2=1. The foci are at (ea, 0) and (−ea, 0), where e is the eccentricity. Each of the two chords of the ellipse passing through a focus and parallel to the minor axis is called a latus rectum and has a length equal to 2b2/a.
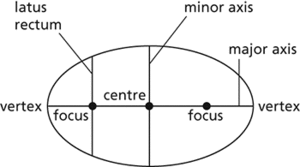
Ellipse.
A particular ‘oval’ shape, informally obtained by stretching or squashing a circle. If it has length 2a and width 2b, its area equals πab.
More precisely, we may define an ellipse as a conic with eccentricity less than 1. Thus, it is the locus of all points P such that the distance from P to a fixed point F1 (the focus) equals e (<1) times the distance from P to a fixed line l1 (the directrix). It turns out that there is another point F2 and another line l2 such that the same locus would be obtained with these as focus and directrix. An ellipse is also the conic section that results when a plane cuts a cone in such a way that a bounded section is obtained (see conic).
The line through F1 and F2 is the major axis, and the points V1 and V2 where it cuts the ellipse are the vertices. The length |V1V2| is the length of the major axis and is usually taken to be 2a. The midpoint of V1 V2 is the centre of the ellipse. The line through the centre perpendicular to the major axis is the minor axis, and the distance, usually taken to be 2b, between the points where it cuts the ellipse is the length of the minor axis. The three constants a, b, and e are related by e2 = 1 − b2/a2. The eccentricity e determines the shape of the ellipse. The value e = 0 is permitted and gives rise to a circle, though this requires the directrices to be infinitely far away, invalidating the focus and directrix description.
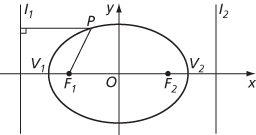
An ellipse in normal form
By taking a coordinate system with origin at the centre of the ellipse and x‐axis along the major axis, the foci have coordinates (ae, 0) and (−ae, 0), the directrices have equations x = a/e and x = −a/e, and the ellipse has equation
where a > b > 0 (see normal form). This ellipse may be parameterized by x = a cosθ, y = b sinθ (0 ≤ θ < 2π) as parametric equations.
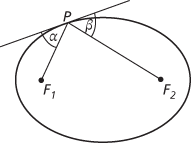
Ellipse highlighting property (ii)
The ellipse has two important properties:
(i) If P is any point of the ellipse with foci F1 and F2 and length of major axis 2a, then |PF1| + |PF2| = 2a. The fact that an ellipse can be seen as the locus of all such points is the basis of a practical method of drawing an ellipse using a string between two points.
(ii) For any point P on the ellipse, let α be the angle between the tangent at P and the line PF1, and β the angle between the tangent at P and the line PF2, as shown in the figure; then α = β. This property is analogous to that of the parabolic reflector (see parabola).
A closed curve like a flattened circle. The orbits of most celestial bodies are ellipses; the body being orbited lies at one focus of the ellipse. The longest diameter of an ellipse is termed its major axis, and the shortest diameter is the minor axis. Half the major axis is the semimajor axis, usually denoted by the letter a; the semiminor axis (half the minor axis) is usually denoted by b. The distance between the two foci of an ellipse divided by the length of the major axis is the ellipse’s eccentricity, e. The eccentricity defines the shape of the ellipse, the ellipse being a circle when e = 0. When e is almost 1, the ellipse is long and narrow. For example, Halley’s Comet follows an orbit for which e = 0.967.
- Hungarian Revolution (23 October–4 November 1956)
- Hungary
- hunger
- Hunger Vulnerability Index
- Hungry Forties
- Huns
- Hunter process
- hunter’s Moon
- Hunt, Henry (1773–1835)
- hunting
- hunting and gathering
- Huntsman process
- Huron
- Huronian
- hurricane
- Hurricane Katrina (2005)
- Husband, Rick Douglas (1957–2003)
- hussar
- Hussein ibn Ali (1856–1931)
- Hussein ibn Talal (1935–99)
- Hussein, Saddam (1937–2006)
- Husserl, Edmund Gustav Albert (1859–1938)
- Huss, John (1372–1415)
- Hutcheson, Francis (1694–1746)
- singular point