A non-parametric test of the null hypothesis that two samples of cyclic data have been drawn from the same population. Suppose the samples contain n₁ and n₂ observations. These observations are first arranged in order of magnitude and then their actual values are replaced by coded values that (working in degrees) are multiples of 360/(n₁+n₂), so that the kth largest value becomes 360k/(n₁+n₂). Let the coded values for the first sample be θ₁, θ₂,…, θ_n1, and calculate R² given by 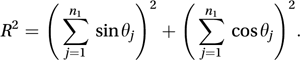The value of R² for the second sample will be identical. The test statistic is T, given by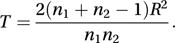For large n₁ and n₂, T has an approximate chi-squared distribution with two degrees of freedom. The test was introduced by Stanley Wheeler and Geoffrey Watson in 1964.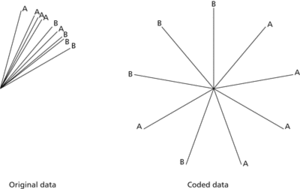

Wheeler–Watson test. Two sets of birds are released from the same location. The five birds in set A fly off in the directions 15°, 25°, 28°, 31°, and 45°. The four birds in set B fly off in the directions 40°, 50°, 52°, and 60°. Arranging these data in order, we have AAAABABBB. Since 360/9=40, the coded values for sample B are (in degrees) 200, 280, 320, and 360. The resulting value for R² is 4.88 and T=3.90. We conclude that there is no significant evidence that the samples have been drawn from different populations.