A measure of the variability in the values of a random variable. In context the word ‘population’ is often omitted. It is defined as the expected value of the squared difference between the random variable and its expected value:
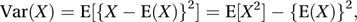
where E(X) denotes the expected value of the random variable X. For a discrete random variable X, taking values x1, x2,…, xn, the variance of X can be calculated as follows:
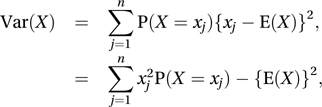where
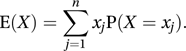For a continuous random variable X, with probability density function f, the variance of X can be calculated as follows:
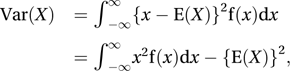where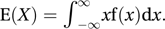
The term ‘variance’ was coined by Sir Ronald Fisher in 1918. Fisher used the symbol σ2, since the variance was the square of the standard deviation that Karl Pearson had denoted by σ in 1894. See Covariance.See also population mean.
- Yorktown
- Yoruba empire of Oyo
- Yoshida Shigeru (1878–1967)
- yotta-
- Youden square
- Youden, William John (1900–71)
- Youden’s index
- Young, Brigham (1801–77)
- Young England
- Younger Dryas
- young fold mountain
- younging
- Young Ireland
- Young Italy
- Young, James (1811–83)
- Young, John Watts (1930–2018)
- Young modulus of elasticity
- young mountain belt crustal type
- Young Plan
- Young, Thomas
- Young, Thomas (1773–1829)
- Young Turks
- Young–Laplace equation
- Young’s inequality
- Young’s modulus