For two random variables X and Y, this is the difference between the expected value of their product and the product of their separate expected values. It is denoted by Cov (X,Y):
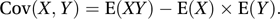
If X and Y are independent then Cov(X, Y)=0. However, if Cov(X, Y)=0 then X and Y may not be independent. A useful result is
Var(aX+bY)=a2Var(X)+2ab Cov(X, Y)+b2Var(Y), where Var denotes variance, and a and b are constants. The term 'covariance' was used by Sir Ronald Fisher in 1930. See also population correlation coefficient.
- domain name server
- domain name service
- Domain Name System
- domain name system
- Domain Name System Security Extensions
- domain name system spoofing
- domain parking
- domain theory
- domain trafficking
- domain wall
- domal uplift
- Dombarovsky Air Base
- dome
- dome and basin
- Domesday Book
- domestic credit expansion
- domestic labour
- domestic product
- domestic rates
- domestic space
- dome–crescent–mushroom
- domichnia
- dominance
- dominance hierarchy
- dominant