A point on a graph y = f(x) at which the concavity (or sense of rotation of the graph) changes. Thus, there is a point of inflexion at a if, for some δ‎ > 0, f″(x) exists and is positive in the open interval (a−δ‎, a) and f″(x) exists and is negative in the open interval (a,a + δ‎), or vice versa.

Inflections that are concave up to concave down

Inflections that are concave down to concave up

If the change (as x increases) is from concave up (anticlockwise rotation) to concave down (clockwise rotation), the graph and its tangent at the point of inflexion look like one of the first three graphs in the figure. If the change is from concave down to concave up, the graph and its tangent look like one of the last three graphs. The second and fourth graph show points of inflexion which are also stationary points.

If f″ is continuous at a, then for y = f(x) to have a point of inflexion at a it is necessary that f″(a) = 0, and so this is the usual method of finding possible points of inflexion. However, the condition f″(a) = 0 is not sufficient to ensure that there is a point of inflexion at a: it must be shown that f″(x) is positive to one side of a and negative to the other side. Thus, if f(x) = x⁴ then f″(0) = 0; but y = x⁴ does not have a point of inflexion at 0 since f″(x) is positive to both sides of 0. Finally, there may be a point of inflexion at a point where f″(x) does not exist, for example at the origin on the curve y = x^1/3, as shown in the figure.

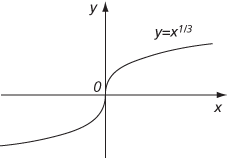
A flex with infinite gradient

If f(x,y,z) is a homogeneous polynomial defining a curve C in a projective plane (see projective space), then a point P on C is a point of inflexion if the Hessian

is zero at P.