Given two lines L and L’ in a projective plane (see projective space) and a point O on neither line, each point P on L can be be associated with a point P’ on L’ such that O,P,P’ are collinear (as in the figure). The bijection from L to L’ sending P to P’ is known as a perspectivity, or the perspectivity from O. By assigning homogeneous coordinates to L and L’, the lines can be identified, and so we can consider perspectivities from a line to itself. The perspectivities of a line generate the projective transformations of the line. See Desargues’ theorem.

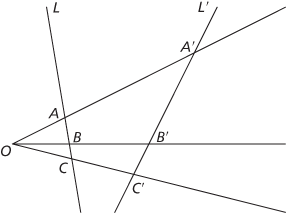
A perspectivity between two lines