“periodogram”的概念、定义、翻译、参考文献-科学参考

periodogram

Statistics

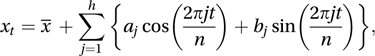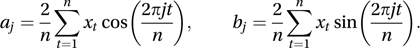A periodogram is a useful graphical tool in the analysis of time series. Consider a time series consisting of n observations x₁, x₂,…, x_n, corresponding to the times t=1, 2,…, n. The mean of the n observations is denoted by x¯. The series may be thought of as resulting from a mixture of cyclic variations of different periodicities so that, for n odd, $periodogram$ where $periodogram$ In the case where n is even the same expressions hold true, but now and there is one additional term in the equation for x_t namely, .
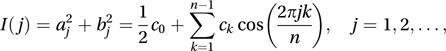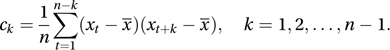The dominating contributions are indicated by large values for a_j or b_j. The periodogram is a plot of I(j) against j, for , where $periodogram$ and $periodogram$ Some authors define the periodogram using multiples (e.g. 2/π) of some of these formulae.
The population counterpart of the time series is the stationary process X(t), and the counterpart of the periodogram is the spectral density function (or power spectrum or spectrum).
The periodogram is not a consistent estimator of the power spectrum and it is usual to give more weight to the first m terms of the summation in the periodogram, using 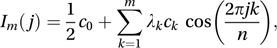$periodogram$ where m<n and the weight λ_k is the lag window. A typical value for m is about . Popular lag windows include:
Bartlett window
k=1, 2,…, m,
Daniell window
k=1, 2,…, m,
Hamming window
k=1, 2,…, m,
Parzen window
1≤k≤½ m,
½m≤k≤m,
Tukey window
k=1, 2,…, m,
Direct analysis of the observed values {x_j} is analysis in the time domain whereas analysis in terms of periodic functions is analysis in the frequency domain.

Computer

In time series analysis, a diagram showing the most important cyclical regularity in the data. Peaks in the diagram correspond to periods of cycles that most closely correlate with the data. Interpretation of periodograms is by spectral analysis.