A measure for judging the extent to which a model explains the variation in a set of data when the parameter estimation is carried out using the method of maximum likelihood. The deviance, D, is given by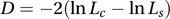where L_c is the likelihood of the current model, and L_s is the likelihood of the saturated model. The deviance has an approximate chi-squared distribution; the number of degrees of freedom is given by the difference in the numbers of parameters in the two models.

A summary of how well a model fits the data is provided by McFadden's R² (which is also known as the likelihood ratio index) defined by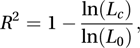where L₀ is the likelihood corresponding to the model that describes the response variable as being a constant unaffected by any explanatory variables. The term ‘deviance’ was introduced by Nelder and Wedderburn in 1972.