A test to determine the nature of stationary points of a function, which uses one or more derivatives of the function. If f ′(α‎) = 0, so there is a stationary point at x = α‎, the first derivative test considers the signs of f ′(x) at x = α‎⁺, α‎⁻, i.e. whether the gradient is positive, negative, or zero as x approaches the stationary point from above and from below. The various possible combinations are shown below.

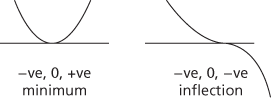
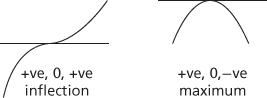
The second derivative test considers the sign of f″(x) at x = α‎. If it is positive, the value of f ′(x) is increasing as the function goes through x = α‎, which requires the stationary point to be a minimum; if f″(α‎) < 0, then it must be a maximum, while if f″(α‎) = 0, it may be that x = α‎ is any of a minimum f(x) = (x–α‎)⁴, a maximum f(x) = –(x–α‎)⁴, or a point of inflection f(x) = (x–α‎)³. To determine the nature in this case, either the first derivative test may be used or higher derivatives can be considered until the first non‐zero higher derivative is found.

See stationary point (in two variables).