| 释义 |
【Hibert空间中随机微分系统稳定性理论】
拼译:the stability theory of stochastic differential systems in Hilbert space
一般受噪声扰动的动态系统的理想数学模型,是20世纪40年代由日本伊藤清建立的随机微分方程。以这种方程描述的系统称为Itô随机微分系统(简称为随机微分系统)。Hilbert空间中的随机微分系统,以更抽象、统一的形式描述了有限维空间中的随机微分系统,随机偏微分系统以及具有滞后的随机微分系统等等。此空间中的随机微分系统稳定性理论就是以近代随机分析理论与方法结合抽象空间中的确定性微分方程稳定性理论与方法,来研究这类系统的李雅普诺夫(Ляпyнов)稳定性理论——各类随机意义下的稳定性分析和判据的建立,Ляпyнов泛函的存在性及其构造以及系统的最优稳定化等等。这样建立起来的稳定性理论,作为特例,不但可应用于上述有限维空间中的各类系统,而且在新的抽象理论基础上,有可能较容易得到新的更深入的结果。 随机系统稳定性理论的建立,一直是以确定性系统稳定性理论为基础,并随着它的发展而发展。Hilbert空间中随机微分系统稳定性理论的建立与发展过程也充分反映了这一历史特征。达特柯(R.Datko)于1968年和1970年首先将有限维空间中确定性常微系统稳定性理论中的Ляпyнов定理[关于霍维茨(Hurwiz)矩阵定理]推广到Hilbert空间上的算子强连续半群。1972年,他又研究了在一般Banach空间中发展方程的一致渐近稳定性。在他工作的基础上,1976年,查柏赛克(J.Zabczyk)研究了无穷维的随机“鲁里叶(Lurie)”型线性系统的稳定性。1978年,豪斯曼(U.G.Haussmann)将Datko的工作推广到了Hilbert空间中的线性随机微分方程:dX+AXdt=B(X)dw, 其中A为可分Hilbert空间H上的强连续半群Ut的线性生成算子,W为可分Hilbert空间K上的维纳(Wiener)过程,其协方差算子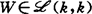 (k到自身的连续线性映射空间)为一正核算子, (k到自身的连续线性映射空间)为一正核算子, 。这一工作也推广了60年代科辛(F.KoZin)关于有限维空间中线性随机微分系统稳定性方面的工作。同年,以柯尔坦(R.F.Curtain)为首的英国沃里克(Warwick)大学控制论中心,以《无穷维线性系统理论》为题,在“Lecture Notes in Control and Information Sciences”,vol.8上,系统地发表了他们在这一领域中的工作。1979年,日本依启卡瓦利用动态规划方法研究了具有状态和控制相关噪声的无穷维线性系统的随机调节器问题和最优平稳控制以及稳定性等。以上这些工作,不仅为Hilbert空间中线性随机微分系统稳定性理论奠定了基础,而且也为Hilbert空间中非线性随机微分系统稳定性理论的发展创造了条件。 。这一工作也推广了60年代科辛(F.KoZin)关于有限维空间中线性随机微分系统稳定性方面的工作。同年,以柯尔坦(R.F.Curtain)为首的英国沃里克(Warwick)大学控制论中心,以《无穷维线性系统理论》为题,在“Lecture Notes in Control and Information Sciences”,vol.8上,系统地发表了他们在这一领域中的工作。1979年,日本依启卡瓦利用动态规划方法研究了具有状态和控制相关噪声的无穷维线性系统的随机调节器问题和最优平稳控制以及稳定性等。以上这些工作,不仅为Hilbert空间中线性随机微分系统稳定性理论奠定了基础,而且也为Hilbert空间中非线性随机微分系统稳定性理论的发展创造了条件。 1982年,Ichikawa在他原来工作的基础上,借助于Hilbert空间中的Ляпyнов函数,研究了下面一类半线性随机发展方程的稳定性:dy=[Ay+f(y)]dt+G(y)dw, 其中:A为实可分Hilbert空间Y上的强连续半群S(t)的无穷小生成算子;f:Y→Y且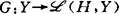 ,均为Lipschitz连续映射;W为实可分Hilbert空间H上具有增量协方差算子W的H-值Wiener过程。他所得到的结果,推广了Haussmann与Curtain的工作。同年,周(P.L.Chow)对下面一类非线性随机发展方程的稳定性也作了研究: ,均为Lipschitz连续映射;W为实可分Hilbert空间H上具有增量协方差算子W的H-值Wiener过程。他所得到的结果,推广了Haussmann与Curtain的工作。同年,周(P.L.Chow)对下面一类非线性随机发展方程的稳定性也作了研究: dy=A(y)dt+B(y)dw, 其中,A:X(实自共轭的Banach空间)→Y(实可分Hilbert空间), ,均为有界连续映射,并且K为实可分的Hilbert空间,使得 ,均为有界连续映射,并且K为实可分的Hilbert空间,使得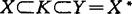 ,均为稠定连续;W仍为具有增量协方差算子W的H-值Wiener过程。他籍助于G0(包含原点) ,均为稠定连续;W仍为具有增量协方差算子W的H-值Wiener过程。他籍助于G0(包含原点)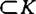 中的一个Ляпунов泛函,建立了该系统的a.s.有界性,a.s.稳定性,a.s.渐近稳定性以及a.s.全局渐近稳定性等判据。 中的一个Ляпунов泛函,建立了该系统的a.s.有界性,a.s.稳定性,a.s.渐近稳定性以及a.s.全局渐近稳定性等判据。 Ichikawa与Chow是较早将稳定性理论中的“Ляпунов直接法”推广到Hilbert空间中随机微分系统稳定性分析中来的两位学者。1983年,Ichikawa在前述Zabczyk(1976)工作的基础上,又进一步研究了随机发展方程的绝对稳定性。他从几个方面推广了1972年莫诺桑(T.Morozan)在有限维情形的工作。1984年,Ichikawa在他1982年工作的基础上,较系统地研究了上述一类半线性随机发展方程的有界性、稳定性和不变测度,所得到的结果推广了1969年(1972,1973)查凯(M.Zakai)和米雅哈拉(Y.Miyahara)在有限维情形的工作。同年,他又发表了关于一类非线性半群的指数稳定性和Lp-稳定性的等价性结果。这一结果不仅可应用于有限维确定性的和随机的微分方程,也可应用于半线性的确定性和随机发展方程,由它可推得已有的相应结果。1984年,Itô的《无穷维空间中随机微分方程基础》,为该领域的研究工作奠定了系统和严格的数学基础。在Ichikawa(1982)工作的基础上,胡宣达于1985年,将稳定性理论中的“比较方法”推广到上述的一类半线性随机发展方程,从而将此类随机发展方程的稳定性在一定的条件下,归结为一类(一维)确定性常微分方程相应稳定性的判定。这不但推广了1982年Ichikawa的相应结果,而且也推广了他本人在有限维情形中的相应工作。1986年,胡宣达又利用比较方法建立了上述一类半线性随机发展方程的各种有界性的比较准则以及不变测度的存在性与唯一性的比较准则;从而将此类随机发展方程不变测度的存在性与唯一性分别与一类(一维)确定性常微分方程的有界性与稳定性建立了直接的联系,并且也推广了上述Ichikawa在1984年工作中的相应结果。1987年,马洪发表了他有关Hilbert空间中随机微分方程解的某些渐近性质的结果。从诸如化学动力学、神经生理学中的众多实际问题来看,只考虑Hilbert空间值的随机过程是不够的,而且从理论上看,考虑可数Hilbert核空间及其对偶比考虑Hilbert或Banach空间更自然也更完美。于是1986年,卡林普尔(G.Kallianpur)等从实际应用中提出了一类可数Hilbert核空间及其对偶空间。嗣后,1987年,佩雷斯-阿伯鲁(V.Pérez-Abreu)在此类核空间中,研究了关于对偶空间值Wiener过程的随机积分。然而此类核空间的对偶空间中的随机分析学基础还是很不完善的,以致不能进一步对此类核空间的对偶空间中的一般随机微分方程的稳定性理论开展研究。为此,胡宣达于1990年,建立了此类核空间的对偶空间中的随机微分概念和Itô公式。1991年,他证明了此类核空间的对偶空间中的前述的一类半线性随机发展方程解的存在唯一性定理。1992年,他又发表了此类核空间的对偶空间中的半线性随机发展方程解的一些性质,等工作。上述工作,为在此类核空间的对偶空间中,进一步研究一般随机微分方程稳定性理论建立了必要的基础。Hilbert空间中随机微分系统稳定性理论仍是一个非常不成熟的研究领域;很多方面的工作,诸如,Ляnунов泛函的存在性及其构造,以及一般非线性系统的最优稳定化等等的研究,至今还未真正涉及。特别是可数Hilbert核空间的对偶空间中随机微分系统稳定性理论的研究,还尚未深入地开展。这一切的一切都有待于今后有志于该领域的研究工作者的努力。【参考文献】:1 Haussmann, U G. J Math Anal Appl. 1978,65;210~2352 Chow PL. JMath Anal Appl, 1992,89;400~-4193 Ichikawa A. J Math Anal Appl,1982,90;12 ~ 444 Hu Xuanda. J of Nanjing Univ Math Biquarterly, 1987,4:1;1~45 Ma Hong, Osaka J Math, 1987,24:2;321~3306 胡宣达.高校应用数学学报,1988,3:2;57~687 胡宣达.南京大学学报数学(半年刊),1992,9:1;8~17(南京大学胡宣达教授撰) |
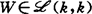 (k到自身的连续线性映射空间)为一正核算子,
(k到自身的连续线性映射空间)为一正核算子, 。这一工作也推广了60年代科辛(F.KoZin)关于有限维空间中线性随机微分系统稳定性方面的工作。同年,以柯尔坦(R.F.Curtain)为首的英国沃里克(Warwick)大学控制论中心,以《无穷维线性系统理论》为题,在“Lecture Notes in Control and Information Sciences”,vol.8上,系统地发表了他们在这一领域中的工作。1979年,日本依启卡瓦利用动态规划方法研究了具有状态和控制相关噪声的无穷维线性系统的随机调节器问题和最优平稳控制以及稳定性等。以上这些工作,不仅为Hilbert空间中线性随机微分系统稳定性理论奠定了基础,而且也为Hilbert空间中非线性随机微分系统稳定性理论的发展创造了条件。
。这一工作也推广了60年代科辛(F.KoZin)关于有限维空间中线性随机微分系统稳定性方面的工作。同年,以柯尔坦(R.F.Curtain)为首的英国沃里克(Warwick)大学控制论中心,以《无穷维线性系统理论》为题,在“Lecture Notes in Control and Information Sciences”,vol.8上,系统地发表了他们在这一领域中的工作。1979年,日本依启卡瓦利用动态规划方法研究了具有状态和控制相关噪声的无穷维线性系统的随机调节器问题和最优平稳控制以及稳定性等。以上这些工作,不仅为Hilbert空间中线性随机微分系统稳定性理论奠定了基础,而且也为Hilbert空间中非线性随机微分系统稳定性理论的发展创造了条件。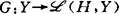 ,均为Lipschitz连续映射;W为实可分Hilbert空间H上具有增量协方差算子W的H-值Wiener过程。他所得到的结果,推广了Haussmann与Curtain的工作。同年,周(P.L.Chow)对下面一类非线性随机发展方程的稳定性也作了研究:
,均为Lipschitz连续映射;W为实可分Hilbert空间H上具有增量协方差算子W的H-值Wiener过程。他所得到的结果,推广了Haussmann与Curtain的工作。同年,周(P.L.Chow)对下面一类非线性随机发展方程的稳定性也作了研究: ,均为有界连续映射,并且K为实可分的Hilbert空间,使得
,均为有界连续映射,并且K为实可分的Hilbert空间,使得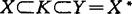 ,均为稠定连续;W仍为具有增量协方差算子W的H-值Wiener过程。他籍助于G0(包含原点)
,均为稠定连续;W仍为具有增量协方差算子W的H-值Wiener过程。他籍助于G0(包含原点)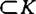 中的一个Ляпунов泛函,建立了该系统的a.s.有界性,a.s.稳定性,a.s.渐近稳定性以及a.s.全局渐近稳定性等判据。
中的一个Ляпунов泛函,建立了该系统的a.s.有界性,a.s.稳定性,a.s.渐近稳定性以及a.s.全局渐近稳定性等判据。